Challenges and Strategies for Mapping Vector Data

Much of the data that we rely on for creating indicators to be included in equity atlases (particularly U.S. Census and American Community Survey data) involve categorizing the attributes of various population groups and mapping them using vectors. This means the data are displayed in pre-set geographic units such as census block groups, census tracts, zip codes, cities or counties. Vector data are mapped using a value that is an aggregation or average of all of the values within a specific geographic unit. The most common reasons for reporting summary values for population data are to ensure individual confidentiality (for the decennial census data) or to maintain data reliability (commensurate with statistical sampling strategies such as those used by the American Community Survey).

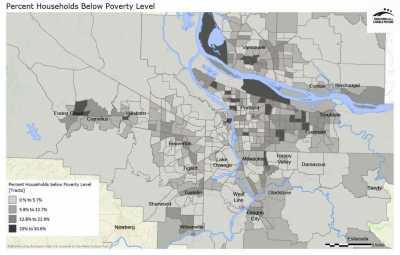
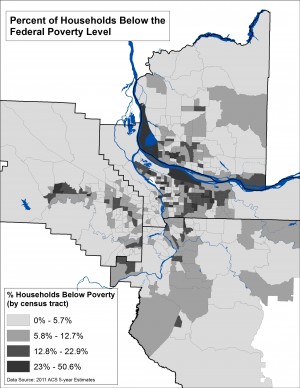
Vector data are often displayed using a choropleth map – a thematic map that uses a single color palette to display the range of data values (a light tint signifies low values, while a dark tint shows high values). For example, the map of poverty in the Regional Equity Atlas 2.0 shows the average poverty rate calculated for each census tract. For more information on choropleth maps, see Applying Cartographic Principles.

Challenges of Vector Maps

Vector maps provide a useful and easy to understand way of presenting essential data, but there are also challenges in developing and interpreting vector maps that should be kept in mind.

Value Distribution: Average or aggregate values are statistically valid measures that provide valuable data about the overall spatial distribution of various phenomena. However, you cannot automatically assume that the value represented within a particular polygon is distributed evenly throughout the polygon’s geographic area. For example, even if there is a high percentage of people in poverty relative to the total population in a given census tract, those people may be concentrated in one part of the census tract rather than evenly distributed across the entire census tract. Conversely, a census tract with a low percentage of poverty overall may still have sub-areas with high numbers of people in poverty. Polygon vector maps are useful for identifying general areas of interest, but groundtruthing (collecting additional data from sample sites on the ground) is often necessary to gather further information about where specific populations are located.

Geographic Resolution: Since census tract boundaries are largely determined by population (with each census tract having approximately 4,000 people), the geographic size of the census tracts can vary widely across a region. Less populated rural areas have very large census tracts, while denser urban areas have smaller census tracts. It is important to remember that the entire census tract will display the color associated with the average value for that tract, giving a strong visual impression that the population, as well, is evenly distributed throughout the entire tract area. While this may be true in dense urban census tracts, the population in large rural census tracts is likely to be concentrated in the few small towns that may be located within the tract. In addition, the sheer size of rural census tracts can also create visual distortions. The smaller urban tracts may display a wider variety of colors or tints within the map, but this pattern can be overshadowed by the larger rural tract, particularly if that tract displays a darker color than most of the small urban tracts. When a map covers a large region (such as the Household Poverty map example above), it is often necessary to create inset maps that zoom into more dense areas so that the more diverse spatial patterns in these areas are more easily observed (see Applying Cartographic Principles for more information).

Normalization of Data: The most common mistake in constructing vector (or choropleth) maps is to use total values (also referred to as “raw” data) rather than data that have been normalized. Normalization refers to the process of standardizing values measured on different scales to a common scale. Normalization is particularly important when mapping spatial data. As discussed above, the area of geographic units such as census tracts can vary widely across a region. Normalization of the data creates a common measure for the “area” variable and is typically achieved by calculating a percent of total (e.g. percent of households in poverty) or density (e.g. population per acre). While there may be some situations in which mapping raw data about populations is appropriate, it is important to note that a map of “totals” can look significantly different than a map that uses the same data, but normalizes the values as “percent of total.”

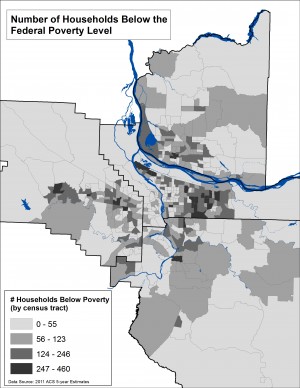
For example, the two maps to the left use the same data about household poverty using the same color palette and classification scheme (“natural breaks” which calculates statistically significant breaks in the range of values based on the number of classes). The first maps the total figures, while the second displays percent of total. While the differences may be subtle, in interpreting these maps remember that they address different kinds of questions. The map of total numbers of households in poverty locates areas that have the highest numbers, without considering these numbers in relationship to the surrounding area. The map that displays percent of households in poverty locates areas where poverty is concentrated.

Choropleth maps based on 2011 American Community Survey data on household poverty mapped by census tracts.
The first map uses the raw totals (total number of households in poverty). The second map displays percent of total.